Los sistemas de dibujo por medio de computadoras tienen la particularidad de depender fundamentalmente de los desarrolladores de software (programas) y hardware (máquinas y accesorios), por lo que sus lógicas están determinadas por políticas empresariales que condicionan, demandando o absorbiendo, diferentes desarrollos académicos o científicos.
En ese contexto, no sería adecuado suponer un estado unificado de sus alcances.
Sin embargo, es posible tomar como referencia algunos casos extensamente aplicados en la práctica para determinar las manifestaciones más evidentes de la aplicación del dibujo axonométrico en los sistemas digitales.
En la mayoría de ellos el dibujo se produce introduciendo información de coordenadas tridimensionales, organizadas por ejes del tipo x-y-z, en un archivo. Esa infomación permite ubicar las posiciones de puntos que definen líneas, líneas que definen superficies y superficies que definen volúmenes.
Esta información constituye un modelo virtual, del que se producen imágenes en pantalla (la pantalla usualmente presenta simultáneamente un listado de coordenadas y comandos y una -o más- imágenes del modelo que se está construyendo).
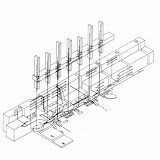
Cada programa se distingue de los demás en primera instancia por la manera de agilizar el proceso constructivo del modelo virtual, incluyendo partes preconstruidas que se insertan, o procedimientos de multiplicación o copia de decisiones ya tomadas, o modos simplicados de transformar el modelo. Usualmente, cada programa también tiende a dar un tipo de imagen del modelo por defecto (o por "default"), es decir, antes de que el usuario tome la decisión de ver el modelo de alguna manera en particular. En general, el modo visual por default que presentan los programas de desarrollo de modelos tridimensionales es el de un dibujo axonométrico, incluyendo los ejes x-y-z y las líneas que construyen el modelo virtual.
Estas condiciones de visualización propias de cada programa, se extienden desde las circunstancias de su producción (la acción de cargar la información del modelo) hacia la actualización de ese modelo en un nuevo archivo, que traduce esa información a una imagen volumétrica opaca, mediante un proceso que informalmente suele llamarse "renderización". Frecuentemente, se emplean programas distintos, especializados, para renderizar los modelos.
En esos procesos, también aparecen mayores diferencias entre los programas, a partir de sus prestaciones para informar sobre condiciones de iluminación, transparencia y apariencias materiales (lo que podríamos llamar sus condiciones de simulación de realismo). Allí es donde se asientan en general los mayores progresos tecnológicos de los programas en cada nueva versión, actualizando las más antiguas tradiciones miméticas del dibujo (aquel rol del dibujo como copia de un registro visual de lo real) dentro de las prácticas más usuales de la perspectiva como proyección cónica.
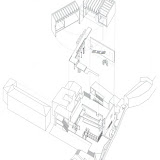
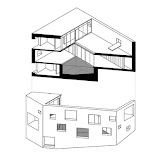
La axonometría sin embargo, parece ocupar en estos sistemas el lugar de la más forma más eficaz para ver la construcción del modelo tridimensional, entender la organización de un conjunto y las relaciones entre sus partes.
En síntesis, también en los modelos digitales, la axonometría tiende a refrendar que su sentido más actual de aplicación es la de un dibujo diagramático, construido a partir de medir y organizar información según tres ejes cartesianos conceptualmente ortogonales, y menos el de una proyección cilíndrica ajustada a la tradición de las perspectivas ópticas, que parecen encontrar otros canales de desarrollo en el presente -los sucedáneos digitales de las perspectivas cónicas-, que analizaremos más adelante.



 .
.
 .
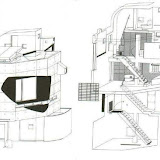
. Extracto de William Curtis. Le Corbusier: Ideas y formas.
Extracto de William Curtis. Le Corbusier: Ideas y formas.